Formula vremena, brzine i udaljenosti: 4. razred. Kako pronaći vrijeme, znajući brzinu i udaljenost? Kako pronaći brzinu ako su poznati vrijeme i udaljenost? Kako pronaći udaljenost ako su poznati vrijeme i brzina? Graf ovisnosti brzine tijela o vremenu

Kako riješiti zadatke gibanja? Formula za odnos između brzine, vremena i udaljenosti. Zadaci i rješenja.

Formula za ovisnost vremena, brzine i udaljenosti za 4. razred: kako se označavaju brzina, vrijeme, udaljenost?

Ljudi, životinje ili strojevi mogu se kretati određenom brzinom. Oni mogu prijeći određeni put u određeno vrijeme. Na primjer: danas možete stići do svoje škole za pola sata. Hodaš određenom brzinom i prijeđeš 1000 metara za 30 minuta. U matematici se put koji se savladava označava slovomS. Brzina se označava slovom v. A vrijeme za koje se prijeđe put označava se slovom t.

• Put —S
• Brzina — v
• Vrijeme —t

Ako zakasniš u školu, može li isto prijeći put za 20 minuta, povećavajući svoju brzinu. To znači da se isti put može prijeći u različitim vremenima i različitim brzinama.

Kako vrijeme putovanja ovisi o brzini?

Što je veća brzina, to će prijeći udaljenost brže. A što je niža brzina, to će duže trajati putovanje.

​​

Kako pronaći vrijeme znajući brzinu i udaljenost?

Kako biste pronašli vrijeme potrebno za prijeđenu udaljenost, morate znati udaljenost i brzinu. Ako udaljenost podijelite s brzinom, znat ćete vrijeme. Primjer takvog zadatka:

Zadatak o zecu. Zec je bježao od Vuka brzinom od 1 kilometra u minuti. Trčao je 3 kilometra do svoje rupe. Nakon nekog vremena Hare je otrčao do rupe?

Koliko je lako riješiti probleme s kretanjem gdje trebate pronaći udaljenost, vrijeme ili brzinu?

1. Pažljivo pročitajte problem i odredite što je poznato iz uvjeta problema.
2. Zapišite ove podatke na nacrt.
3. Također napišite što je nepoznato i što treba pronaći
4. Koristite formulu za probleme udaljenosti, vremena i brzine
5. Unesite poznate podatke u formuli i riješiti zadatak

Rješenje zadatka o zecu i vuku.

• Iz uvjeta zadatka utvrđujemo da znamo brzinu i udaljenost.
• Iz uvjeta zadatka također određujemo da trebamo pronaći vrijeme koje je trebalo zecu da otrči do rupe.

Zapisujemo ove podatke u nacrt na primjer:

Udaljenost do rupe — 3 kilometra

Brzina zeca — 1 kilometar u 1 minuti

Vrijeme je nepoznato

Zapišimo sada isto matematičkim simbolima:

J— 3 kilometra

V — 1 km/min

t—?

Prisjećamo se i zapisujemo formulu za određivanje vremena u bilježnicu:

t = S: v

Sada zapisujemo rješenje zadatka brojevima:

t = 3: 1 = 3 minute

Kako pronaći brzinu ako su poznati vrijeme i udaljenost?

Da bismo pronašli brzinu, ako su poznati vrijeme i udaljenost, udaljenost se mora podijeliti s vremenom. Primjer takvog zadatka:

Zec je pobjegao Vuku i pretrčao 3 kilometra do svoje rupe. Tu je udaljenost prešao za 3 minute. Koliko je brzo zec trčao?

Rješenje problema kretanja:

1. U nacrtu pišemo da znamo udaljenost i vrijeme.
2. Iz uvjeta zadatka određujemo da trebamo pronaći brzinu
3. Podsjetimo se formule za pronalaženje brzine.

Formule za rješavanje takvih problema prikazane su na slici ispod.

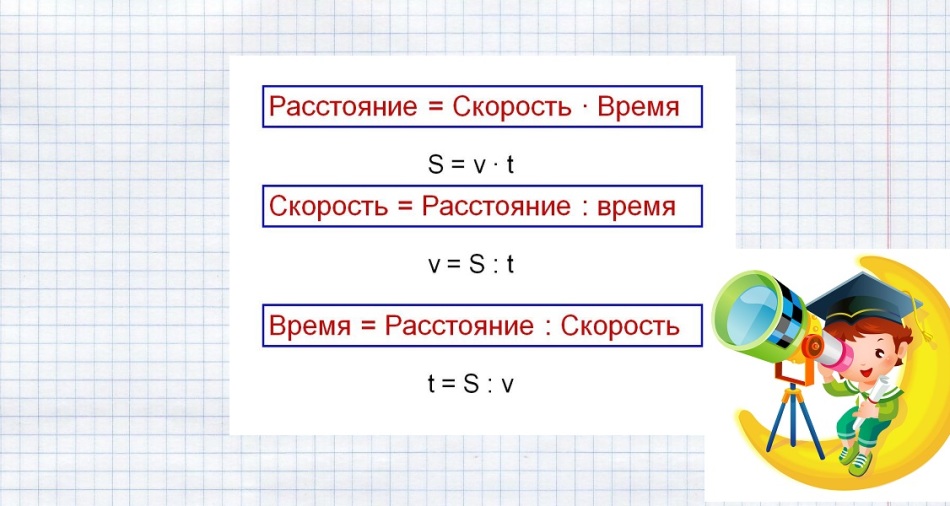
Zamijenite poznate podatke i riješite zadatak:

Udaljenost do rupe je 3 kilometra

Vrijeme koje je Zecu trebalo da stigne do rupe bilo je 3 minute

Brzina je nepoznata

Zapišimo ove poznate podatke matematičkim simbolima

S— 3 kilometra

 t— 3 minute

v —?

Napišemo formulu za pronalaženje brzine

v = S: t

Zapišimo sada rješenje zadatka brojevima:

v = 3: 3 = 1 km/min

Kako pronaći udaljenost ako je vrijeme a brzina se zna?

Da biste pronašli udaljenost, ako su poznati vrijeme i brzina, pomnožite s brzinom. Primjer takvog zadatka:

Zec je bježao Vuku brzinom od 1 kilometar u 1 minuti. Trebalo mu je tri minute da dotrči do rupe. Koliko je zec pretrčao?

Rješenje zadatka: U nacrt upisujemo ono što znamo iz uvjeta zadatka:

Brzina Zeca je 1 kilometar. u 1 minuti

Vrijeme dok je zec dotrčao do rupe - 3 minute

Udaljenost - nepoznata

Sada, zapišimo isto matematičkim simbolima:

v — 1 km/min

t— 3 minute

S —?

Podsjećamo na formulu za određivanje udaljenosti:

S = v ⋅ t

Zapišimo sada rješenje zadatka brojevima:

S = 3 ⋅ 1 = 3 km

Kako naučiti rješavati složenije zadatke?

Da biste naučili rješavati složenije zadatke, morate razumjeti kako rješavati jednostavne, zapamtiti koji znakovi označavaju udaljenost, brzinu i vrijeme. Ako se ne možete sjetiti matematičkih formula, trebali biste ih zapisati na komad papira i uvijek imati pri ruci kada rješavate zadatke. S djetetom rješavajte jednostavne zadatke koje možete smisliti u hodu, primjerice u šetnji.

Mjerne jedinice

​​

Pri rješavanju zadataka o brzini, vremenu i udaljenosti često pogriješe jer zaborave preračunati mjerne jedinice.

VAŽNO: Mjerne jedinice mogu biti bilo koje, ali ako u istom zadatku postoje različite mjerne jedinice, pretvorite ih u iste. Na primjer, ako se brzina mjeri u kilometrima u minuti, tada udaljenost mora biti prikazana u kilometrima, a vrijeme u minutama.

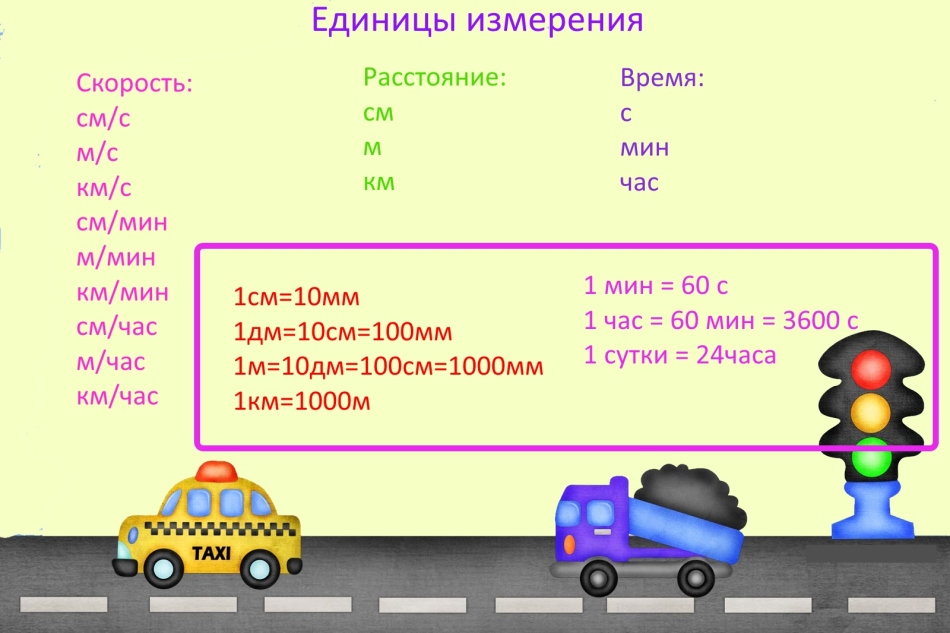
Za znatiželjne : Općeprihvaćeni sustav mjera naziva se metrički, ali to nije uvijek bio slučaj, pa su se u drevnoj Rusiji koristile druge mjerne jedinice.

Problem Boa : Slon i majmun izmjerili su duljinu boa u koracima. Krenuli su jedno prema drugom. Brzina majmuna bila je 60 cm u jednoj sekundi, a brzina bebe slona 20 cm u jednoj sekundi. Na mjerenje su potrošili 5 sekundi. Kolika je duljina boe? (rješenje ispod slike)

<> Rješenje:

Iz uvjeta zadatka utvrđujemo da znamo brzinu majmuna i slona i vrijeme koje im je trebalo da izmjere duljinu boe.

Zapišimo ove podatke:

Brzina majmuna je 60 cm/s

Brzina slona je 20 cm/s

Vrijeme — 5 sekundi

Udaljenost nepoznata

Zapišimo ove podatke matematičkim simbolima:

v1 — 60 cm/s

v2 — 20 cm/s

t — 5 sekundi

S —?

Zapišimo formulu za udaljenost, ako su poznati brzina i vrijeme:

S = v ⋅ t

Izbrojimo udaljenost koju je prešao majmun:

S1 = 60 ⋅ 5 = 300 cm

Sada izbrojimo koliko je slončić prešao:

S2 = 20 ⋅ 5 = 100 cm

Zbrajamo udaljenost koju je prešao majmun i udaljenost koju je prešao slon:

S = S1 + S2 = 300 + 100 = 400 cm

Grafikon ovisnosti brzine tijela o vremenu: fotografija

Udaljenost pokriveno različitim brzinama pokriveno je u različitim vremenima. Što je veća brzina, to je manje vremena potrebno za kretanje.

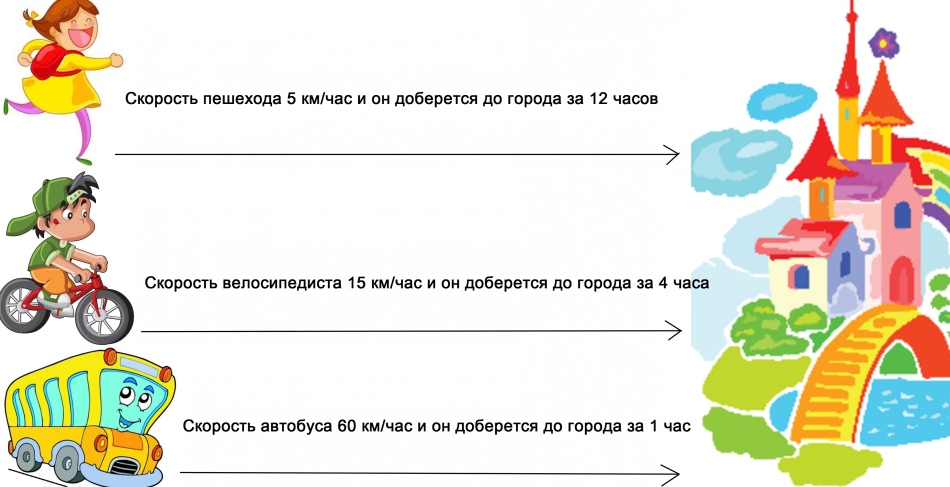
Tablica 4 klasa: brzina, vrijeme, udaljenost

Br	Brzina (km/h)	Vrijeme (sat)	Udaljenost (km)
1	5	2	?
2	12	?	12
3	60	4	?
4	?	3	300
5	220	?	440

Možete maštati i smišljati zadatke za stol sebe. Ispod su naše opcije za uvjete zadataka:

1. Mama je poslala Crvenkapicu baki. Djevojčica je stalno bila rastresena i hodala je kroz šumu polako, brzinom od 5 km/h. Na putu je provela 2 sata. Koliko je Crvenkapica prešla za to vrijeme?
2. Poštar Pečkin nosio je paket na biciklu brzinom od 12 km/h. On zna da je udaljenost između njegove kuće i kuće strica Fedora 12 km. Pomozite Pečkinu izračunati koliko će trajati putovanje?
3. Papa Ksyusha kupio je auto i odlučio odvesti obitelj na more. Automobil se kretao brzinom od 60 km/h i na putu je proveo 4 sata. Kolika je udaljenost između Ksyushine kuće i morske obale?
4. Patke su se skupile u klin i odletjele u tople krajeve. Ptice su neumorno mahale krilima 3 sata i za to vrijeme prešle 300 km. Kolika je bila brzina ptica?
5. Zrakoplov AN-2 leti brzinom od 220 km/h. Poletio je iz Moskve i leti za Nižnji Novgorod, udaljenost između ta dva grada je 440 km. Koliko dugo će avion biti na putu?

Odgovore na zadane zadatke možete pronaći u tablici ispod:

Br.	Brzina (km/h))	Vrijeme (sat)	Udaljenost (km)
1	5	2	10
2	12	1	12
3	60	4	240
4	100	3	300
5	220	2	440

Primjeri rješavanja zadataka brzine, vremena, udaljenosti za 4. razred

Ako u jednom zadatku postoji više objekata koji se kreću, trebate naučiti dijete da promatra kretanje tih objekata odvojeno, a tek onda zajedno. Primjer takvog zadatka:

Dva prijatelja Vadyk i Tema odlučili su otići u šetnju i napustili su svoje kuće kako bi se sreli. Vadyk je vozio bicikl, a Tema je hodala. Vadyk je vozio brzinom od 10 km/h, a Tema je hodala brzinom od 5 km/h. Sat vremena kasnije sreli su se. Kolika je udaljenost između Vadikove i Temine kuće?

Ovaj se problem može riješiti pomoću formule za ovisnost udaljenosti o brzini i vremenu.

S = v ⋅ t

Udaljenost koju Vadyk prijeđe na biciklu bit će jednaka njegovoj brzini pomnoženoj po vremenu u prolazu.

S = 10 ⋅ 1 = 10 kilometara

Udaljenost koju je Subjekt prešao izračunava se na sličan način:

S = v ⋅ t

Zamijenite digitalne vrijednosti njegove brzine i vremena u formulu

S = 5 ⋅ 1 = 5 kilometara

Udaljenost koju je prešao Vadyk mora se dodati udaljenosti koju je prešao Tema.

10 + 5 = 15 kilometara

Kako naučiti rješavati složene probleme koji zahtijevaju logično razmišljanje?

Za razvoj logičkog mišljenja djeteta potrebno je iz njih rješavati jednostavne, zatim složene logičke zadatke. Ovi se zadaci mogu sastojati od nekoliko faza. Možete prijeći iz jedne faze u drugu samo ako je prethodna riješena. Primjer takvog zadatka:

Anton je vozio bicikl brzinom od 12 km/h, a Lisa je vozila skuter brzinom 2 puta manjom od Antonove, a Denis hodala brzinom 2 puta manjom od Lisine. Kolika je Denisova brzina?

Za rješavanje ovog problema potrebno je prvo znati Lisinu brzinu, a tek onda Denisovu brzinu.

Dva biciklista krenula su iz različitih gradova u susret. Jedan od njih je žurio i jurio je brzinom od 12 km/h, a drugi je vozio ležerno brzinom od 8 km/h. Udaljenost između gradova iz kojih su biciklisti krenuli je 60 km. Koliko će svaki biciklist prijeći prije nego što se sretnu? (rješenje ispod fotografije)

Rješenje:

• 12+8 = 20 (km/h) je ukupna brzina dvojice biciklista, odnosno brzina kojom su se približavali jedan drugom
• 60: 20 = 3 (h) je vrijeme nakon kojeg su se biciklisti susreli
• 3 ⋅ 8 = 24 (km) je udaljenost koju je prešao prvi biciklist
• 12 ⋅ 3 = 36 (km) je put koji je prešao drugi biciklist
• Provjera: 36+24=60 (km) je put koji su prešla dva biciklista.
• Odgovor: 24 km, 36 km.

Ponudite djeci da u obliku igre riješe sljedeće zadatke. Možda će htjeti sami napraviti problem oko prijatelja, životinja ili ptica.

VIDEO: Problemi s kretanjem